A Skeptic’s Guide to Scientific Writing

Stefano Allesina QuEST Workshop, U. Vermont, Apr 2021

History of the paper

The way of publishing research has been evolving over the past few centuries:

• First journal in 1665 Philosophical Transactions of the Royal Society; rudimentary editorial review; initially, many short articles describing oddities and events (Of the way of killing ratle-snakes, used in Virginia, An observation imparted to the noble Mr Boyle, by Mr David Thomas, touching some particulars further considerable in the monster mentioned in the first papers of these philosophical transactions ).
• Starting in 1753, papers for PTRS were read by a fellow at a Society meeting, and considered by a Committee on Papers: “There were four possible verdicts: a paper might be printed, rejected, consideration of it deferred to a future meeting, or referred to someone more expert – in which case the Committee could call upon an ordinary member of the Society, who would sit in on the relevant meeting and vote not just on the specific paper he’d been called to give an opinion on but on all papers considered at that meeting. (This was not very widely applied, but it is the first instance of provision for peer review being written into the statutes of the Society).” (from here).
• Books continued to dominate until 19th century, with physical sciences being the first to transition to journal-dominated.
• External, anyonymous reviews started sometimes in the 19th century, but became customary much later.
• Einstein, who had submitted to Physical Reviews in 1935: “We (Mr. Rosen and I) had sent you our manuscript for publication and had not authorised you to show it to specialists before it is printed. I see no reason to address the – in any case erroneous – comments of your anonymous expert. On the basis of this incident I prefer to publish the paper elsewhere.”
• Right now: Editor (or Deputies) sift through submissions (desk-rejections are common); assign to a specialist editor (typically, member of the Editorial Board), who selects 2-4 reviewers. Outcomes: accept, minor revisions, major revisions, reject (with or without prejudice).
• Some special cases: Watson and Crick paper on the structure of DNA was not reviewed before publication.
• Open access, published reviews, accompanying code and data, registered experiments, reproducible papers are contemporary inventions.

Common advice on writing papers

The advice given to scientific writers follows closely that given to journalists:

• keep it short
• keep it simple
• who/what/where/when (also, how!)
• write for your audience
• write to be understood

Advice on how to write from Boyle, who was the main proponent of scientific communication based on short essays (rather than books): a Philosopher need not be sollicitous that his style should delight its Reader with his Floridnesse, yet I think he may very well be allow’d to take a Care that it disgust not his Reader by its Flatness, especially when he does not so much deliver Experiments or explicate them, as make Reflections or Discourses on them; for on such Occasions he may be allow’d the liberty of recreating his Reader and himself, and manifesting that he declin’d the Ornaments of Language, not out of Necessity, but Discretion, which forbids them to be us’d where they may darken as well as adorn the Subject they are appli’d to.

Just looking at “10 simple rules” PLoS CB:

• Bourne, 2005, Ten Simple Rules for Getting Published
• Zhang, 2014, Ten Simple Rules for Writing Research Papers
• Mensh & Kording, 2017, Ten simple rules for structuring papers
• Penders, 2018, Ten simple rules for responsible referencing
• Rougier et al., 2014 Ten Simple Rules for Better Figures
• Pautasso, 2013, Ten Simple Rules for Writing a Literature Review
• Frassi et al., 2018, Ten simple rules for collaboratively writing a multi-authored paper

What works for me

• Writing takes much longer than typing.
• Work on the structure of the narrarive on a piece of paper; choose a few figures and connect the dots; try this with multiple people.
• Extensively document what you’re doing (RMarkDown, Jupyter notebook, literate programming).
• Start from the Supplementary information.
• Writing as “carving” vs. “building”. (“I saw the angel in the marble and carved until I set him free.” — Michelangelo)

Pet peeves and best practices

Things that I value as a reviewer:

• line numbers, please!
• no poetic/enigmatic titles
• if you are using data, include them
• if you are using code, include it (and make it readable)
• if you are using interesting/novel techniques, be pedagogical (at least in SI)
• cite relevant work
• put care in preparing figures/text

Things that I value as an editor:

• clearly state the problem you want to solve
• it is better if the problem existed before you solved it
• make a clear case for the choice of journal
• do not overstate relevance/novelty
• include suggestions for handling/academic editors and reviewers

Being a skeptic

Weinberger, Evans & Allesina, 2015, Ten Simple (Empirical) Rules for Writing Science

Is the advice given to scientists any good?

• Take 1M abstracts from a variety of disciplines
• Count citations (as a proxy for readership)
• Measure features of the abstract (e.g., length, active vs. passive, how many words are “simple”)
• Use z-scores (to account for differences in journals)
• Build a linear model to account for year of publication, journal, discipline, number of authors, paper length
• Do certain features correlate with the number of citations?

Have some fun with real data

The file data/plos_compbio.csv contains data on all the documents published in PLoS Computational Biology (as of 3/3/2021). The file is comma-separated, with headers specifying the content of each column:

• DOI the Digital Object Identifier for the document
• title the title of the document
• year the publication year
• num_citations number of citations received (Scopus data)
• num_views number of views for the html/pdf version of the document
• document_type type of document (see below)
• num_authors number of authors
• num_references number of references cited in the document
• num_figures number of figures in the document
• num_equations obtained counting special math formatting in XML source of the document
• num_countries number of distinct countries in affiliation list
• num_words_title number of words in the title
• num_words_abstract number of words in the abstract
• prop_words_abs proportion of distinct words in the abstract that are found in a list of words used for spell-checking (~0.5M words)
• prop_simple_words_abs proportion of distinct words in the abstract that are found in a list of words used in simplified English (~2K words)
• first_au_F probability that first author is a woman (see below)
• last_au_F probability that last (senior) author is a woman (see below)

The file data/plos_compbio_details.csv contains:

• DOI the Digital Object Identifier for the document
• abstract the full text of the abstract (for documents with an abstract)
• countries the list of countries represented in the affiliation list
• subjects a list of (self-reported) subjects
• reference_years the years in which the cited references were cited

Notes on data

Obligatory disclaimer: data are never perfect.

Missing data (e.g., for documents without abstract) is reported as NA.

You can read a document by opening https://journals.plos.org/ploscompbiol/article?id=YOUR_DOI_HERE for example https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1000494

Types of documents

• Article: 7173
• Editorial: 155
• Erratum: 150
• Review: 149
• Short Survey: 15
• Letter: 14
• Note: 13
• Conference Paper: 6

Assignment of gender is based on first name. The reported probability is computed by counting the number of newborns that were assigned at birth a certain name and sex combination (as of today, SSA reports only male/female). The data, provided by the Social Security Administration, covers US newborns from about 1880 to today. Clearly, the assignment is going to be most accurate for authors residing in English-speaking countries, though the large immigrant population in the US allows some resolution of names that originated in other areas of the world.

Taking a peek

This rich data set allows us to explore several aspects of scientific writing. Just a few basic visualizations:

# the code for the visualizations below is here
source("../data_viz/simple_visualizations.R")

Distribution of citations:

pl_cit1

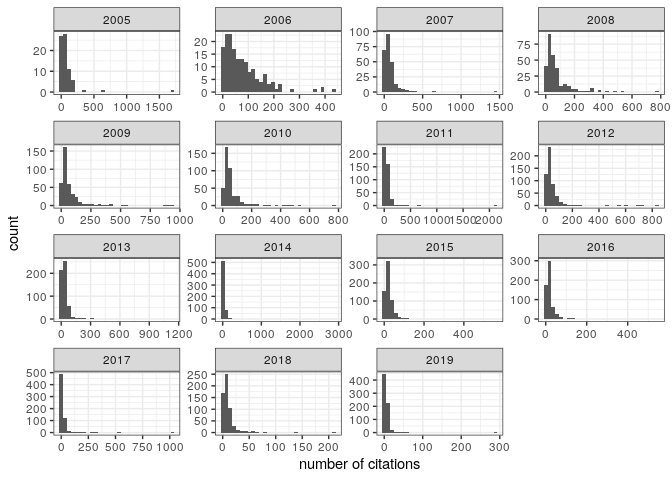
Note the very broad, skewed distribution. To model citations, it is therefore convenient to transform the data. In particular, plotting log(num_citations + 1), we obtain:

pl_cit2

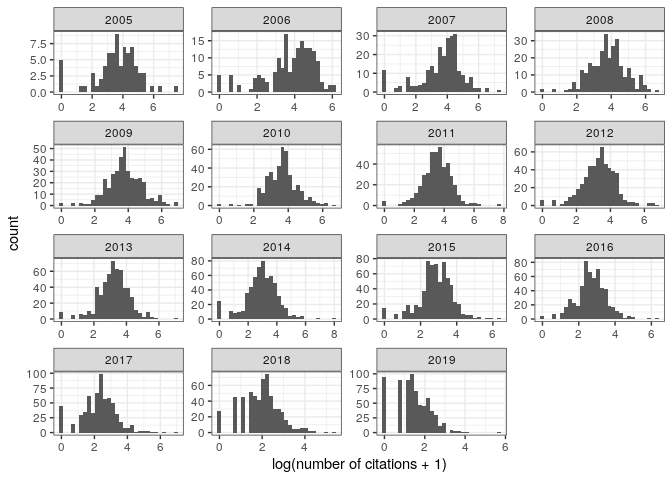
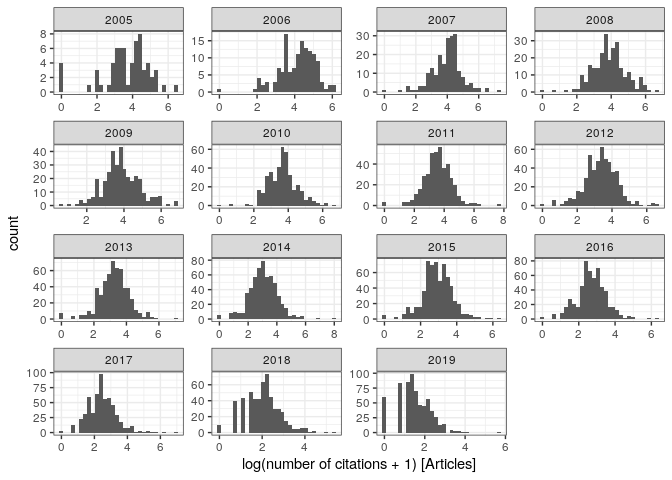
Note the many documents with zero citations—these are mostly editorials, errata, etc. Considering only Article, we find Gaussian-looking distributions (note that 2020 and 2021 are excluded):

pl_cit3

Similarly, the number of views is highly skewed:

pl_view1

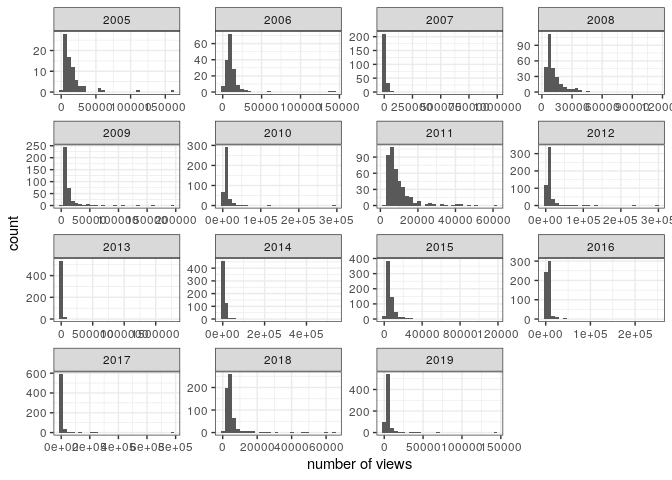
and the transformation has a similar effect:

pl_view3

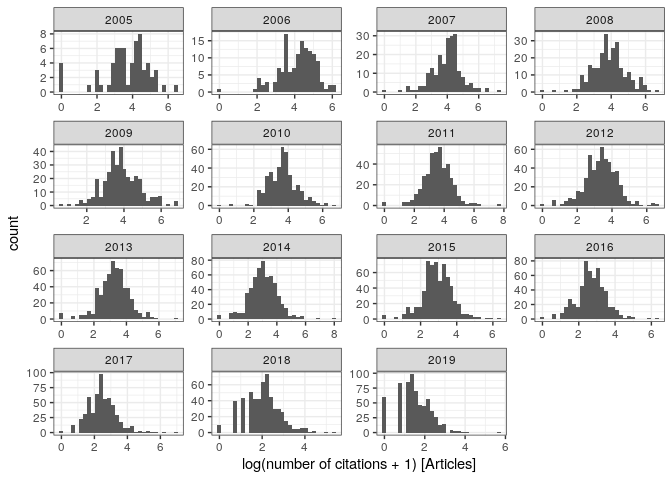
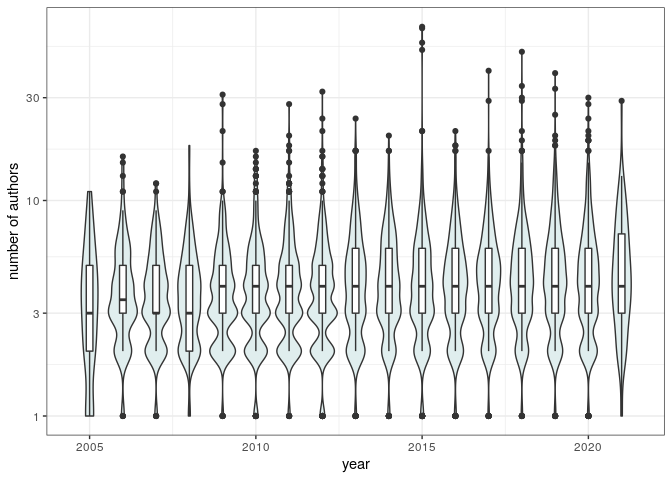
The typical number of authors per document increased slightly over the years (record holder):

pl_au

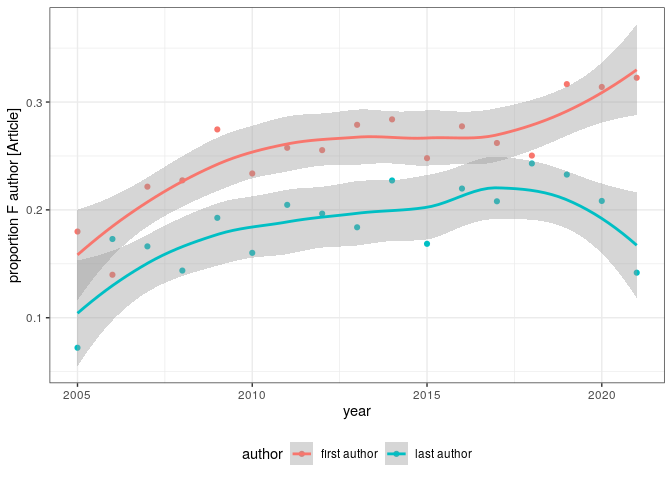
And the proportion of articles authored by women about doubled over 15 years:

pl_gender

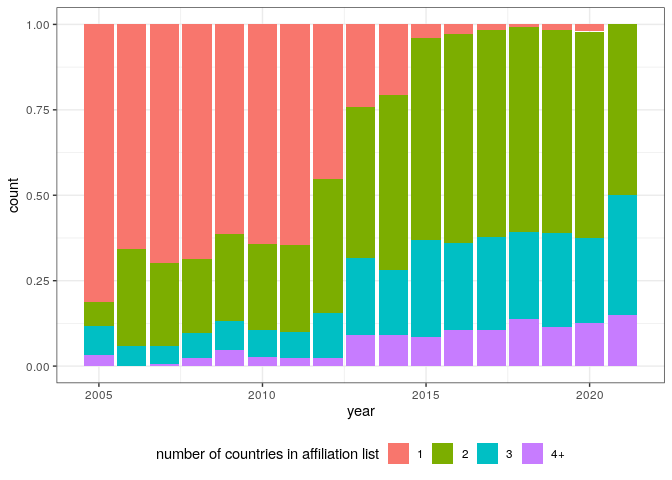
International collaborations became more frequent (record holder):

pl_countries

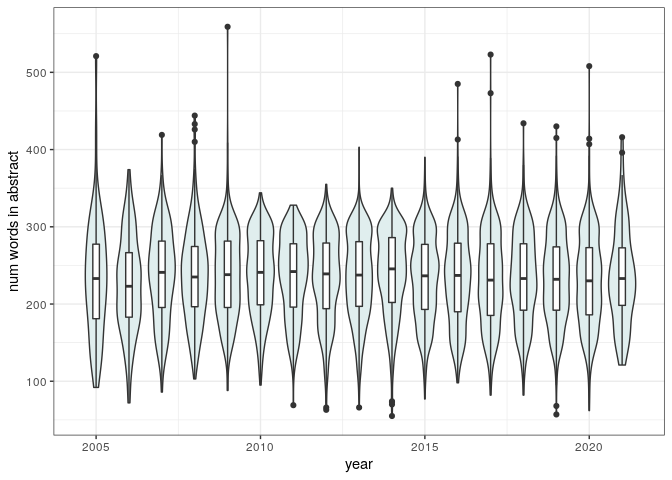
The number of words in the abstract has remained about constant (record holder):

pl_abs_len

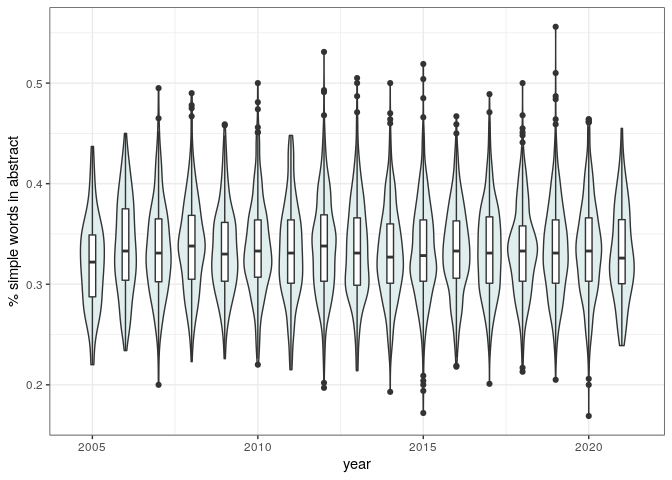
The proportion of simple words in the abstract has also remained quite constant:

pl_simple_words

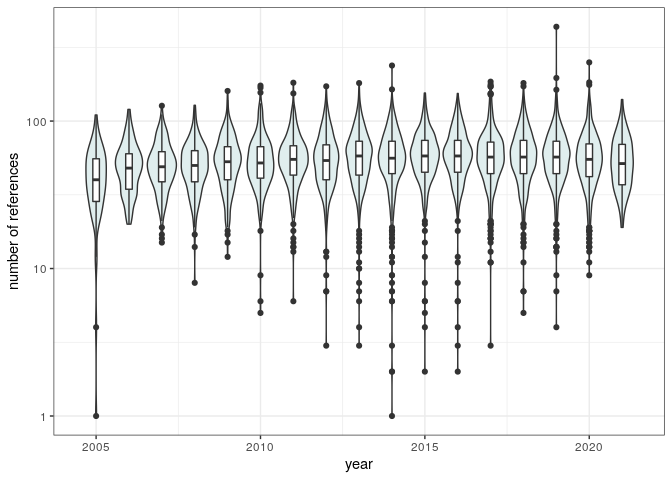
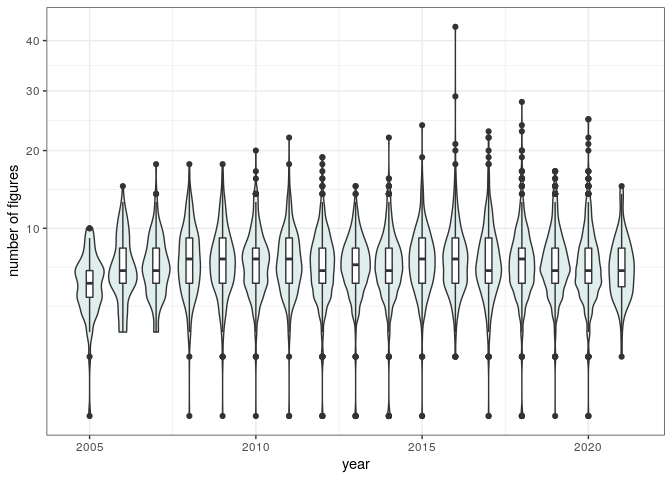
The number of references and figures has been constant as well (record holder):

pl_num_refs

pl_num_figs

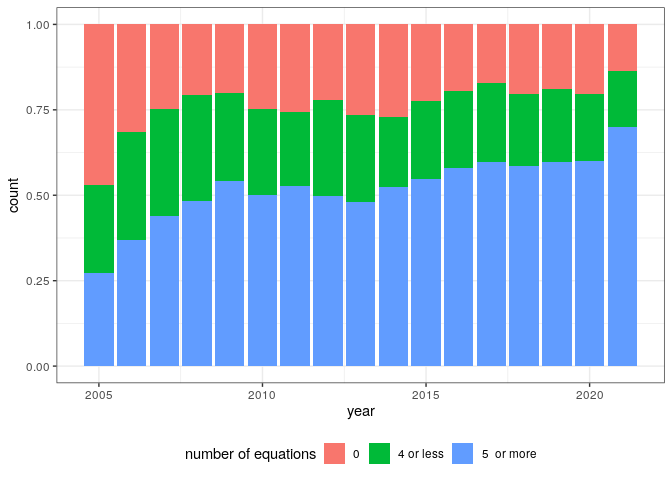
While the proportion of articles containing several equations has been growing steadily (record holder):

pl_num_eqn

Choose your own adventure

• Effect of shorter titles (based on Letchford et al. “The advantage of short paper titles” Royal Society open science 2015)

• Effect of equations (based on Fawcett and Higginson “Heavy use of equations impedes communication among biologists” PNAS 2012)

• Effect of figures (based on Lee et al. “Viziometrics: Analyzing visual information in the scientific literature.” IEEE 2017)

• International collaborations (based on Smith et al. “The scientific impact of nations: Journal placement and citation performance” PLoS ONE 2014)

• Your question here (maybe inspired by Tahamtan et al. “Factors affecting number of citations: a comprehensive review of the literature” Scientometrics 2016)

A Choice of Weapons

Rank-correlation

Does a certain feature correlate (in a qualitative/ranking sense, e.g. Kendall’s) with citations/view?

• Pros: easy, quick to compute, easy to interpret, works well for highly skewed distributions (such as citations/views).
• Cons: difficult to control for factors influencing the response (e.g., number of authors, year of publication); one possibilty is to split the data into classes and run it by class.

Generalized Linear Models

Take (y_i) to be the (possibly, log-transformed) number of citations (or views) for article (i). We can model this “response variable” as a linear combination of the predictors, and an error term. Examples (in R):

log(num_citations + 1) ~ year (assumes that citations increase at a constant rate by year)

log(num_citations + 1) ~ as.factor(year) + num_authors (fit each year independently, assumes citations change in an orderly, exponential [i.e., the log is linear] way with the number of authors; you might want to bin the number of authors and use it as a factor)

The model can be made as complex as needed.

• Pros: well-studied, quick to compute, excellent diagnostics.
• Cons: need careful transformation of response variable; model selection to choose among several competing models; changes in order and detailed implementation of predictors can change result.

Randomizations

Say that we want to probe whether papers with a female first-author accrue more citations than those with a male first-author. Then we can compute the average (or median, etc.) number of citations for papers with a female first author. Call this the observed average. Then, we can re-compute the value after shuffling the imputed sex of the first author in the data. By repeatedly shuffling and measuring, we create a distribution of the expected average number of citations. If the observed value lies in the tails of the distribution (e.g., measure a p-value), we conclude that the effect of having a female first-author is significant.

• Pros: very robust, easy to understand and implement.
• Cons: computationally intensive; it is easier to test for binary predictors.

Homework

Analyze the provided data, guided by an hypothesis on what would make for an impactful paper. If you share an Rmd file with me, I can publish it on the website for next week.

An example, looking at homophily in co-authorship.